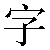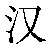Learn Chinese for Free—Lesson 15
Today's Chinese characters:
一两个位人
The other Chinese characters contained in this lesson have already been studied previously. You can just click on them and go back to the corresponding lesson.
Today's last character looks like a man walking, doesn't it? Welcome, Mr. Long-Legs!
In this lesson, you're going to know what a measure word is and how to use two of them.
| Character Knowledge Meter |
|---|
|
18.1%
Today with this lesson your knowledge of Chinese characters will reach 18.1% of all the Chinese language usage! |
Characters' Essentials

两 is generally used before measure words.
Don't use 二.



Description and Examples
Question 1: "One person"用中文怎么说?
Question 2: "Two persons"用中文怎么说?
Let's answer the first question. Since you already know how to write "one" and I just told you that today's last character means "person", you may be tempted to say that the Chinese for "one person" is:
![]()
Sorry, it's wrong. In modern Chinese, a measure word is generally needed between a numeral and a noun. What's a measure word?
Measure words are words used as unit of measurement for people, things or verb's actions.
For example, Chinese language has specific measure words for:
- books;
- certain animals;
- stick-like things;
- things with a handle;
- indicating the number of times a verb's action repeats...
A measure word is generally needed between a numeral and a noun. So, the correct Chinese phrase for "one person" is:
一个人 translation: one person
Suggestion: roll the mouse pointer over each character and read its pinyin.
Change of tones: A few characters change their tone under certain circumstances. 一, for example, when alone or at the end of a word or a sentence, is pronounced in the first tone; when it precedes a syllable of the first, second or third tone, it is pronounced in the fourth tone; it is pronounced in the second tone when it is followed by a fourth tone. For this reason, the phrase above is pronounced yí gè rén. |
Other examples, without translation (your first test!):
三个人
十个人
九十九个人
Did you notice? The Chinese for "person" is 人, and the Chinese for its plural "persons" is 人 as well! So, forget English language rules about plurals! |
The other measure word, 位, is used only with people, indicating respect. The following two phrases have almost the same meaning, the first one denoting respect.
一位人 translation: one person
一个人 translation: one person
When we say that 位 is used before people, it means that we can also say, indicating respect:
一位老师 translation: a teacher
一位医生 translation: a physician
Let's answer now the second question, "two persons"用中文怎么说?
Well, the following phrase IS WRONG.
![]()
I heard you. Wrong? Why?!?
The usage of 二 and 两, even if they both mean two, is different. 二 is generally not used before measure words.
Infact, the correct Chinese phrase for "two persons" is:
两个人 translation: two persons
You now don't need any translation of the following phrases, do you? If you still do need the English translation, my suggestion is to spend a few minutes reviewing this course first lessons.
一个医生
一位老师
两位老师
十一个医生
一百零五位医生
Do you often forget a character's meaning or pronunciation? I'd be surprised if you don't! SOLUTION (only in the online version of this course): click on the character or on the word and a little window will pop up with its pinyin and a link to the lesson that explained it. |
Our next object is to learn how to write the sentence: "She's my teacher."
Learning this sentence will help you to master:
- Chinese personal pronouns;
- How to use the verb to be;
- How to use the #1 most used Chinese character 的.
Tomorrow you'll learn some more Chinese personal pronouns, including "she".
Is there anything you want to ask me about this lesson?
That's all for today. I wish you like my website and go on clicking and clicking on its other sections! However, if you need personalized lessons and want to make your pronunciation perfect click here.
IMPORTANT: About the ads in this page, if you see something inappropriate please tell me immediately (even anonymously) clicking here. |